
The ratio of sides in a 30°−60°−90° right triangle is x: x : 2 x. Because the perimeter is 60 inches, and the three sides are equal in measure, then each side is 20 inches (60 ÷ 3 = 20). If an altitude is drawn, it creates two 30°−60°−90° right triangles. The hypotenuse is 16.įigure 7 Using the longer leg of a 30°−60°−90° triangle to find the hypotenuse.Įxample 6: Find the length of an altitude in an equilateral triangle with a perimeter of 60 inches.įigure 8 is an equilateral triangle. x is the longer leg, and it is opposite the 60°. In Figure 7 , the shorter leg, x, is opposite the 30°. Consequently, the other two sides must be 4 A and 2(4), or 8.įigure 6 Using the shortest side of a 30°−60°−90° triangle to find the remaining sides.Įxample 5: If the longer leg of a 30°−60°−90° right triangle is 8, find the length of the hypotenuse. The other two sides are then x (opposite the 60°) and 2 x (opposite the 90°). The side opposite 90° is the longest side (hypotenuse) and is 2 or 2 x.Įxample 4: If the shortest side of a 30°−60°−90° right triangle is 4, what is the measure of the other two sides?

The side opposite 30° is the shortest side and is 1 or x (Figure 5).įigure 5 The ratios of the sides of a 30°−60°−90° triangle The ratio of the sides of a 30°−60°−90° right triangle is 1 : : 2 or x : x : 2 x placed as follows. A 30°− 60°− 90° right triangle has a unique ratio of its sides. Therefore, this is an isosceles right triangle with the ratio of sides x : x : x Because one leg is 10, the other must also be 10, and the hypotenuse is 10, so y = 10 and z = 10. Therefore, each side of the square has a measure of 6.Ĥ5° + 90° + x° = 180° (The sum of the angles of a triangle = 180°.) x = 45° 6 represents the hypotenuse.Įxample 3: What are the measurements of x, y, and z in Figure 4 ?įigure 4 Finding the unknown parts of this right triangle So x = 6, and each side of the square has a measure of 6. The ratio x : x : x for isosceles right triangles can now be applied where x = 6. Look at Figure 3 .įigure 3 A diagonal of a square helps create two congruent isosceles right triangles. Method 1: The diagonal of a square divides it into two congruent isosceles right triangles. Using the Pythagorean Theorem and the fact that the legs of this right triangle are equal,Įxample 2: If the diagonal of a square is 6, find the length of each of its sides.
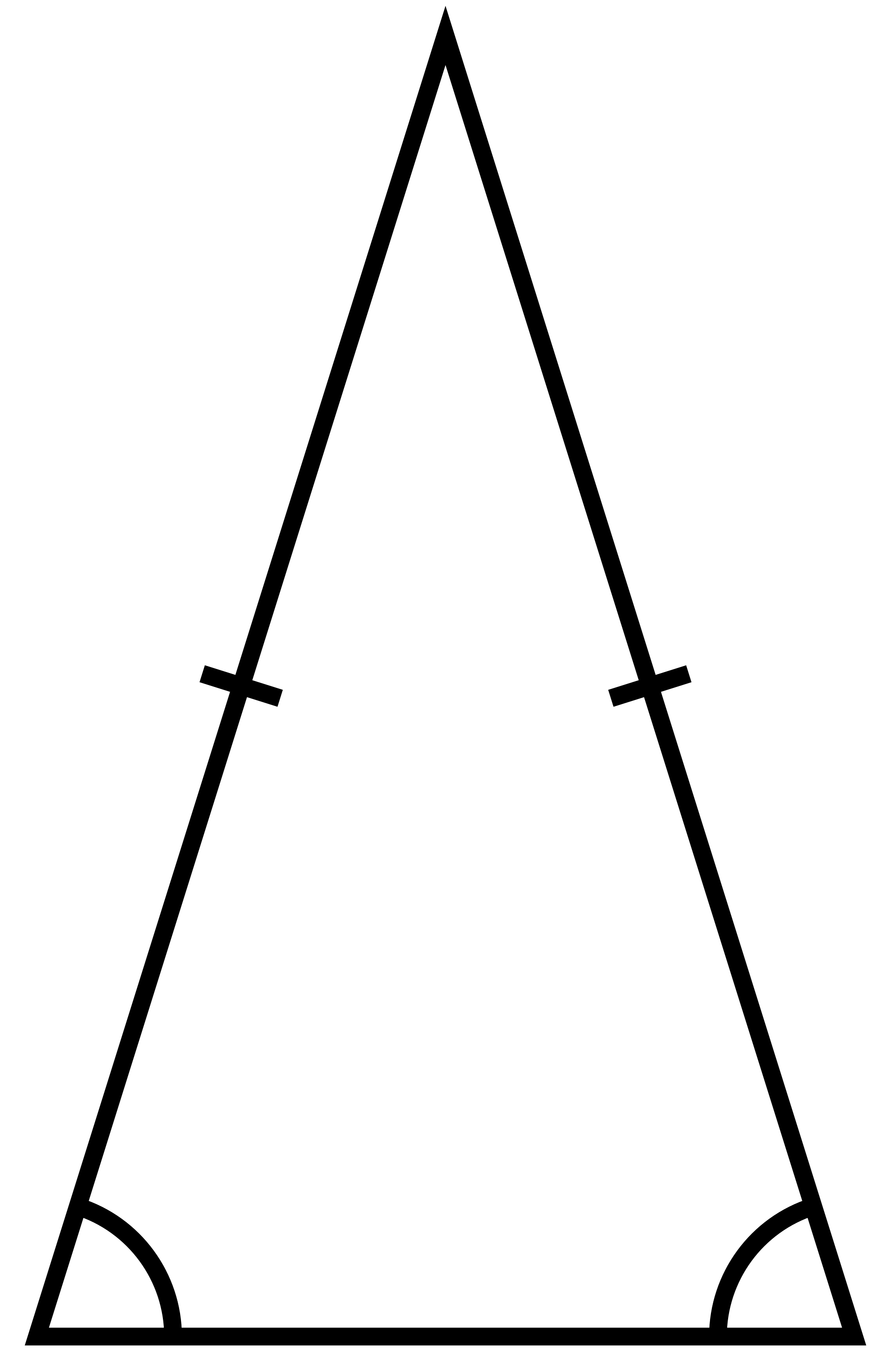
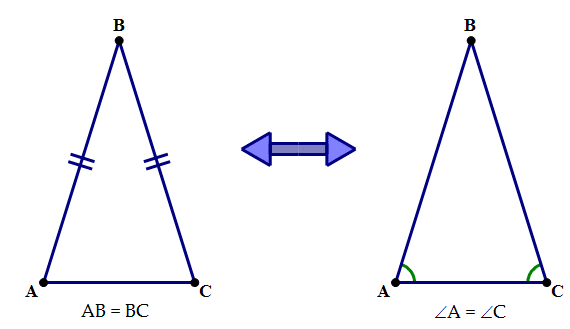
Method 1: Using the ratio x : x : x for isosceles right triangles, then x = 3, and the other sides must be 3 and 3. The ratio of the sides of an isosceles right triangle is always 1 : 1 : or x : x: x (Figure 2 ).įigure 2 The ratios of the sides of an isosceles right triangleĮxample 1: If one of the equal sides of an isosceles right triangle is 3, what are the measures of the other two sides? (The right angle cannot be one of the equal angles or the sum of the angles would exceed 180°.) Therefore, in Figure 1 , Δ ABC is an isosceles right triangle, and the following must always be true. It has two equal sides, two equal angles, and one right angle. An isosceles right triangle has the characteristic of both the isosceles and the right triangles. Angles may be inscribed in the circumference of the circle or formed by intersecting chords and other lines. Summary of Coordinate Geometry FormulasĬentral angles are probably the angles most often associated with a circle, but by no means are they the only ones.Slopes: Parallel and Perpendicular Lines.Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Proving that Figures Are Parallelograms.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.Classifying Triangles by Sides or Angles.
Lines: Intersecting, Perpendicular, Parallel.


 0 kommentar(er)
0 kommentar(er)
